零多項式

在之前的講解，也曾簡單地提到了零多項式，現在就深入介紹什麼是零多項式。
首先給大家看一個例子，假設零多項式的域是H，所以多項式的例子可以為: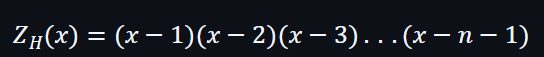

大家可以輕易地留意到當 x = 1 時，整個多項式為零，當 x = 2 時，整個多項式也為零，當 x 去到 n-1 時，整個多項式也為零。

為了進一步講解，會利用另一多項式 P(x)及 Z(x) 做說明，假設存在一個多項式 P(x)，當x為它的根時，它可以被另一多項式 ZH(x) 整除，及不會有餘數: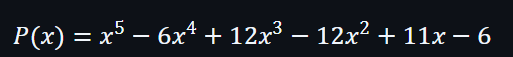

及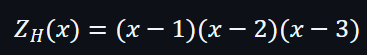

再進一步，可以將P(x)簡化: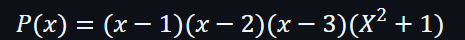

簡化之後，可以留意到多項式 P(x) 在從 1 到 3 的時候，P(x)會等於 0。
因此多項式 Zh(x) 能讓證明者有一個對於從 1 到 3 的時候存在一個為零的多項式。
如果在整除過程後的多項式有餘數，就表示在計算過程中存在錯誤。
另外，為什麼不能有餘數，另一原因是因為在有餘數的情況下，證明者無法使用可信任設定中的公共參考字串來產出證明。
例如這例子: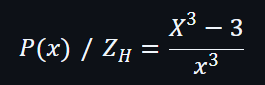

如果除法後有餘數，這就沒法在橢圓曲線上計算出相關的值，雖然可以可以將除法轉為以負數的次方形式表示，從而求解。
不過在 CRS 是針對正數次方來計算出來的。

如果一個程式需要 5 個步驟來計算或驗證某些內容，這就需要創建一個對於所有相關的狀態都是等於 0 的零多項式。
一般來說 zk-SNARK 程式可能需要 100 萬個步驟(或者可以理解為"門")才能產生證明。對於證明者來說，創建和利用比較長的多項式，直接地會對證明者的效率產生很大影響。
例子:

類似的多項式，可以在 Groth16 看到。
然而，PLONK 的就不同，會使用乘法子群，它也是建立在單位根上的。